四元数知识汇总

作者

这个话题是最近开始学习和总结的，力求把四元数的基础相关知识汇总完。在大学的时候就偶尔听到过四元数，不过由于没有实际使用，就没过多的深入了解。机缘巧合，最近在工程代码里看到了关于四元数的计算相关代码，顺藤摸瓜，就把四元数的前世今生都搜了搜，学习和记录下，以备以后使用。

什么是四元数？

四元数的来历是在复数的基础上经过几十年偶然发展来的，我们用\(a+bi\)表示复数，二元数，其中\(i^{2} =-1\)。四元数是在复数的基础上增加了\(j\)和\(k\)，由Hamilton在1843年发现的。

一个四元数\(q\) 可以被定义以下形式，相互等价。

$$q=a+bi+cj+dk = a + \vec{v} , (a,b,c,d \in \mathbb{R} )$$

其中，\(\vec{v} = bi+cj+dk = (b,c,d)\)

i^2=j^2=k^2=-1,\quad jk=-kj=i,\quad ki=-ik=j,\quad ij=-ji=k

\(a\)为四元数\(q\)的实部， \(vec{v}\) 是虚部， \(i,j,k\) 为虚数单位(imaginary units)。

以上是一些基本概念，其中\(i,j,k\)的相乘转换结果，看起来毫无头绪，我们将它放在三维坐标里可以发现规则。可以通过建立坐标和右手法则得出，我们以\(ki\)为例，可以理解为将\(i\)左乘\(k\)变换，大拇指方向为\(k\)方向，将\(i\)转动90°，得到的结果是\(j\)，\(ki=j\)。其他相乘类似，你可以试一下。

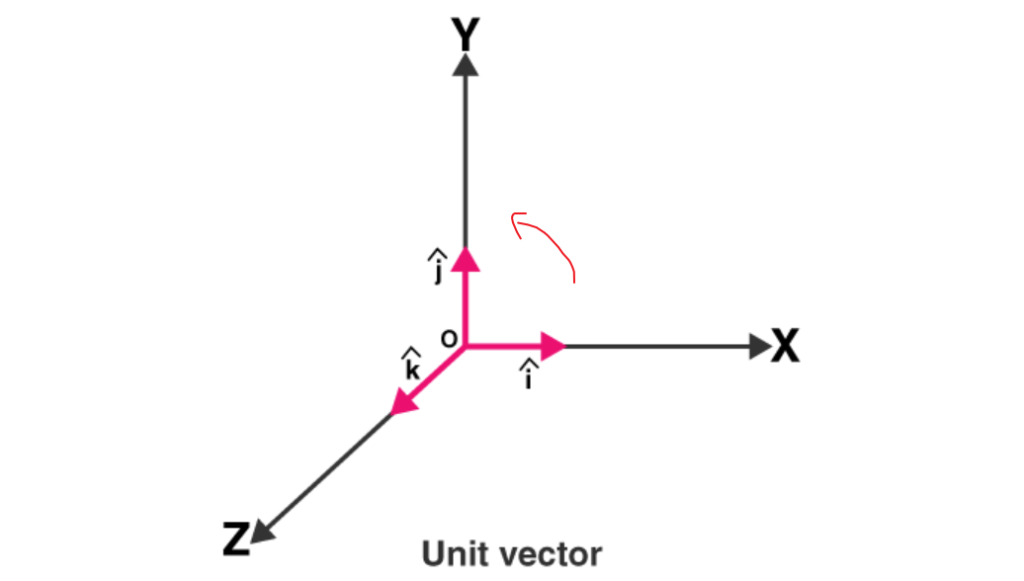
一些性质

  • 模长：\(\parallel q\parallel = \sqrt{（a^{2} +b^{2}+c^{2}+d^{2}）} = \sqrt{(a+v\cdot v)}\)
  • 共轭：虚部取反即可。\(q=a-bi-cj-dk \)
  • 纯四元数：实部为0的四元数，即\(q=0+bi+cj+dk\)
  • 单位四元数：模长为1的四元数

四元数四则运算

首先四元数的乘法运算不满足交换律，即一般情况下：\(pq \ne qp\)

四元数的加减: 对应部分相加相减。

四元数的乘法：对应项相乘，然后利用

i^2=j^2=k^2=-1,\quad jk=-kj=i,\quad ki=-ik=j,\quad ij=-ji=k
进行化简。

四元数的除法：一般对四元数不做除法，用逆取而代之。

四元数的逆

当\(q\)为单位四元数时，模长为1，逆与共轭相同，这种方式求逆比较简洁。

四元数可视化

3Blue1Brown通俗易懂的视频推荐，需要多看几遍。

四元数点乘

float QuaternionMath::QuaternionDot(const Quaternion &a, const Quaternion &b)
{
  float rt = a.w * b.w + a.x * b.x + a.y * b.y + a.z * b.z;
  return rt;
}

这段代码是一个计算两个四元数的点乘的函数实现。给定两个四元数 \(a\) 和 \(b\)，它们的点乘定义为：

$$
\text{dot}(a, b) = a.w \cdot b.w + a.x \cdot b.x + a.y \cdot b.y + a.z \cdot b.z
$$

其中，\(a.w, a.x, a.y, a.z\) 分别表示四元数 \(a\) 的实部和虚部分量，\(b.w, b.x, b.y, b.z\) 分别表示四元数 \(b\) 的实部和虚部分量。

函数中的代码实现了这个点乘的计算，并返回结果。即先将四元数的对应分量相乘，然后将它们相加得到最终的结果。该函数返回的结果是一个浮点数。

点乘的意义：

四元数的点乘（dot product）是指两个四元数之间进行元素对应相乘，并将结果相加得到一个标量值的操作。点乘在四元数中有以下含义：

  1. 量化两个四元数之间的相似度：点乘可以用来衡量两个四元数之间的相似度或相关性。如果两个四元数的点乘结果接近于1，则它们表示的方向相似或平行；如果点乘结果接近于-1，则它们表示的方向相反；如果点乘结果接近于0，则它们表示的方向垂直或无关。
  2. 判断四元数是否归一化：点乘可以用来检查四元数是否归一化。如果一个四元数是单位四元数（长度为1），则它与自身的点乘结果为1。因此，通过计算一个四元数与自身的点乘，可以验证它是否已经被归一化。
  3. 计算四元数的长度（模）的平方：点乘的结果可以用来计算四元数的长度（模）的平方。如果一个四元数为 \(q = a + bi + cj + dk\)，则它的长度的平方为 \(|q|^2 = a^2 + b^2 + c^2 + d^2\)。点乘 \(q \cdot q\) 的结果恰好等于四元数的长度的平方。
  4. 判断四元数是否共线：如果两个四元数的点乘结果为0，则它们表示的方向垂直，可以判断它们不共线。如果点乘结果不为0，则可以判断它们共线，并且点乘的结果的正负号可以表示它们的相对方向。

总的来说，四元数的点乘提供了一种度量、判断和计算四元数之间关系的方法，包括相似度、长度、共线性等。

四元数与旋转矩阵

用四元数的主要目的就是要表示3D旋转，空间三维旋转。

空间三维旋转矩阵的表示形式有欧拉角、轴角和四元数。欧拉角的形式比较多，根据旋转顺序的不同有旋转矩阵有不同的结果，但是有万向死锁的问题存在，丢失自由度。

动图

那么我们用四元数如何表示3D旋转呢？

假设一个向量\(v\)沿着旋转轴\(u\)旋转\(θ\)°之后的向量为\({v}’\)，那么可以用四元数表示这个旋转\(q=[cos(\theta /2),sin(\theta /2)u]\)，令\(\upsilon =[0, v]\) 纯四元数，那么可以得到向量经过旋转后的向量（纯四元数）为

$${\upsilon}’ =qvq^{*} = qvq^{-1}$$

我们四元数中的角度，真实对应两倍的旋转角度。具体分析可以参考本文末尾的PDF。

由以上分析之后，可以很轻松的通过单位四元数，得到旋转的轴角。

$$q=[a,b ]\\
\theta /2 = cos^{-1}(a)\\
\vec{v} = \frac{b}{sin(cos^{-1}(a))}$$

四元数的插值

首先说明，为什么要插值？

我们在设置目标物体旋转时，比如从A姿态变换到B姿态，对于变换过程中的姿态该如何平滑的转动呢？考虑到均匀匀速等，插值的目的是让整个姿态的旋转过程平滑过渡。

四元数的插值包括三种：线性插值Lerp(Linear Interpolation)、正规化线型插值Nlerp(Normalized Linear Interpolation)、球面插值Slerp(Spherical Linear Interpolation)。

对于两个四元数夹角很小的情况使用Nlerp，对于夹角很大的情况，先进行点乘判断夹角大小，如果方向相反，则先对任意一个四元数取反。那么为什么取反，四元数表示的矩阵相同呢？即\(q与-q\)表示的旋转是一样的。

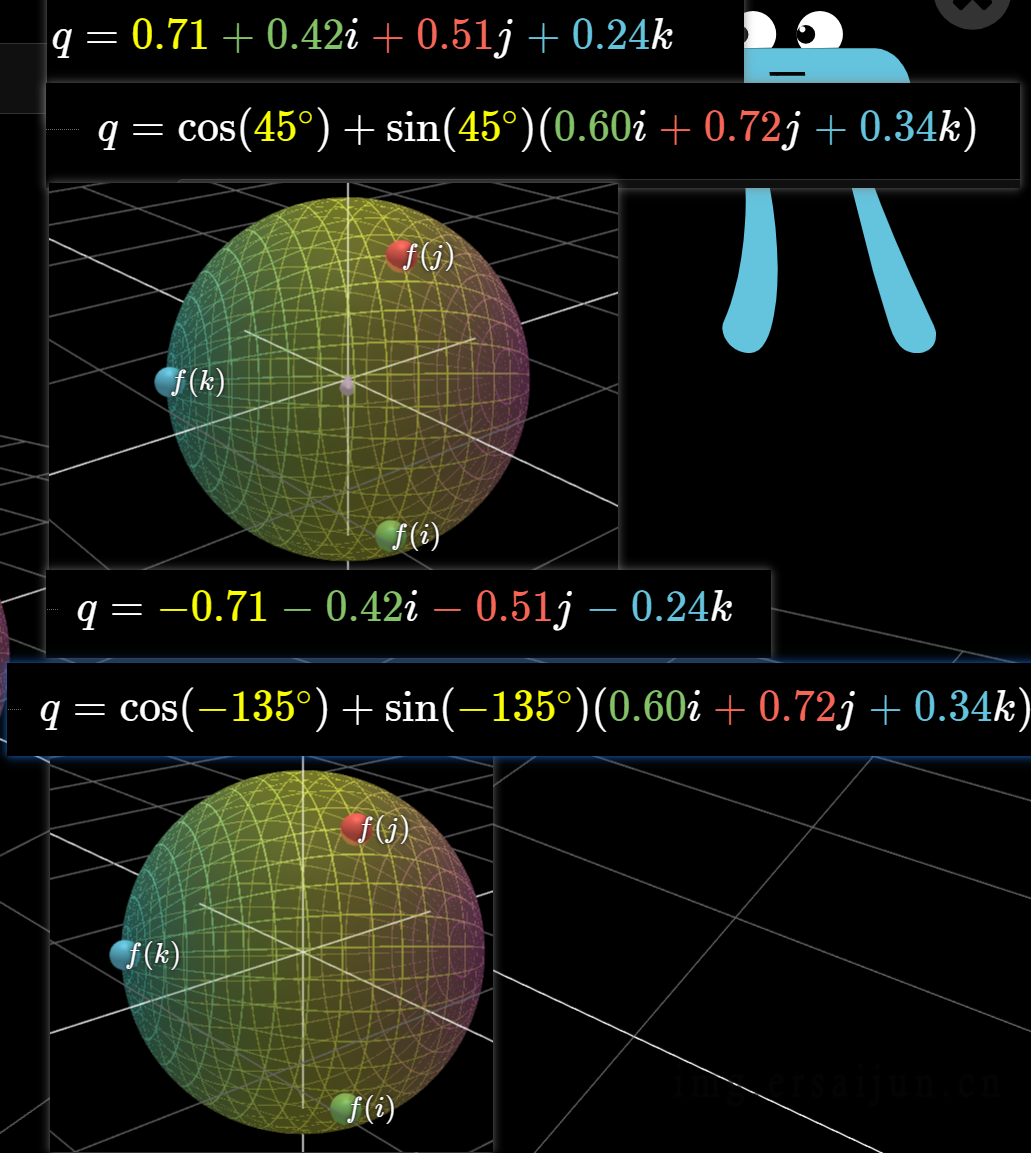
以上图片是我截取的视频里的，可以看到q与-q在空间中的旋转是一致的。

  • 线性插值
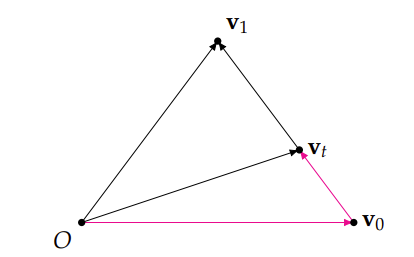
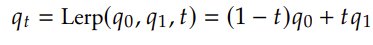
  • 正规化线型插值
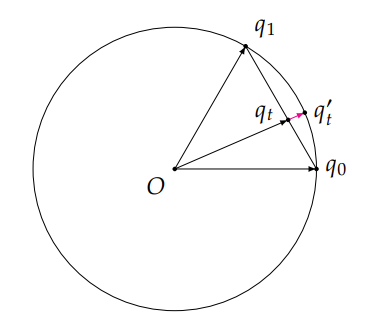
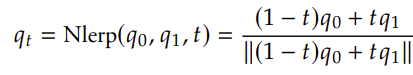
  • 球面插值

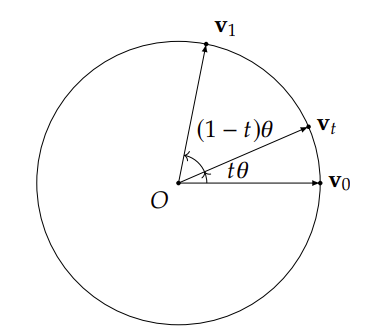
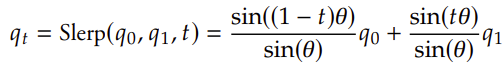
代码实现

C++
#include <Eigen/Dense>

Eigen::Quaterniond slerp(const Eigen::Quaterniond& q1, const Eigen::Quaterniond& q2, double t) {
    // 归一化四元数
    Eigen::Quaterniond q1_normalized = q1.normalized();
    Eigen::Quaterniond q2_normalized = q2.normalized();
    
    // 判断方向是否一致，如果不一致则取反
    if (q1_normalized.dot(q2_normalized) < 0) {
        q2_normalized = -q2_normalized;
    }
    
    // 计算角度差和插值权重
    double dot_product = q1_normalized.dot(q2_normalized);
    double theta = std::acos(dot_product);
    double sin_theta = std::sqrt(1 - theta * theta );
    
    // 如果角度差较小，使用线性插值
    if (std::abs(sin_theta) < 1e-8) {
        return (1 - t) * q1_normalized + t * q2_normalized;
    }
    
    double weight1 = std::sin((1 - t) * theta) / sin_theta;
    double weight2 = std::sin(t * theta) / sin_theta;
    
    // 执行球面插值
    Eigen::Quaterniond interpolated = q1_normalized * weight1 + q2_normalized * weight2;
    return interpolated.normalized();
}

// 注：以上代码由ChatGPT生成

推荐阅读附录中的交互视频和文档，会有更多的收获。

以上是整体的关于四元数的全部内容了，如果有没涉及到的部分，我会在以后的时间更新本文。

二赛君整理，转载请注明地址和出处。

附录

Visualizing quaternions, an explorable video series (eater.net)【推荐】

四元数与三维旋转-Krasjet【推荐】

quaternion下载

Related posts:

Interactive Quaternion Calculator | 转换可视化交互
Interactive Linear Algebra
3D Rotation Converter | 3维旋转变换
Introduction to the A* Algorithm

发表评论